Hallo Sahabat SIMAK UI

Tentu kamu sudah tidak asing dengan persamaan lingkaran bukan? Lingkaran adalah salah satu bentuk geometri yang paling sederhana, tetapi juga memiliki sifat dan karakteristik yang menarik. Untuk memahami dan memanfaatkan lingkaran dalam matematika, kita perlu memahami persamaan lingkaran, kaidah-kaidahnya, cara menentukan persamaan lingkaran, serta rumus-rumus bantu yang terkait.

baca juga : les privat

Apa Itu Lingkaran?

Sebelum kita masuk ke dalam persamaan lingkaran, mari kita pahami apa itu lingkaran. Lingkaran adalah himpunan semua titik yang memiliki jarak yang sama dari titik tertentu yang disebut sebagai pusat. Jarak ini disebut sebagai jari-jari (r) dan jarak dari pusat ke tepi lingkaran disebut sebagai radius.

Rumus Bantu dalam Persamaan Lingkaran

Ada beberapa rumus bantu yang dapat membantu dalam memahami dan menyelesaikan masalah yang melibatkan lingkaran:

1. Luas Lingkaran (A): Rumus luas lingkaran adalah A = π, di mana r adalah panjang radius lingkaran.
2. Keliling Lingkaran (C): Rumus keliling lingkaran adalah C = 2πr atau C = πd, di mana r adalah panjang radius dan d adalah diameter lingkaran.
3. Hubungan Diameter dan Radius: Diameter (d) adalah dua kali panjang radius, yaitu d = 2r.
4. Panjang Busur Lingkaran: Untuk menghitung panjang busur lingkaran, kita dapat menggunakan rumus panjang busur s = θ/360° × 2πr, di mana θ adalah sudut dalam derajat di tengah lingkaran.
5. Rumus Titik di Luar atau di Dalam Lingkaran: Untuk menentukan apakah suatu titik berada di dalam atau di luar lingkaran, kita dapat menggunakan persamaan (x – + (y – < Untuk titik di dalam lingkaran dan (x – + (y – >  Untuk titik di luar lingkaran.

Sifat penting dari persamaan lingkaran

Beberapa sifat penting dari persamaan lingkaran dan bagaimana mereka berperan dalam dunia matematika dan kehidupan sehari-hari.

Bentuk Umum Persamaan Lingkaran: Persamaan lingkaran dalam bentuk umumnya dinyatakan sebagai: (x−+(y−=r2(x−+(y−=r2 di mana (h, k) adalah koordinat titik tengah lingkaran dan r adalah jari-jari lingkaran. Bentuk ini menggambarkan semua titik (x, y) yang memiliki jarak tetap r dari titik tengah (h, k).
Titik Tengah dan Jari-jari: Koordinat (h, k) adalah titik tengah lingkaran, yang juga merupakan pusat lingkaran. Jari-jari (r) adalah jarak dari pusat lingkaran ke tepi lingkaran. Semakin besar nilai r, semakin besar lingkaran tersebut. Sebaliknya, jika r = 0, maka lingkaran tersebut akan menjadi titik tunggal di titik tengah (h, k).

Sifat Geometri Lingkaran:

1. Lingkaran selalu simetris terhadap pusatnya. Ini berarti, jika titik (x, y) berada pada lingkaran, maka titik (h – x, k – y) juga akan berada pada lingkaran.
2.  Semua titik pada lingkaran memiliki jarak yang sama ke pusatnya. Inilah yang membedakan lingkaran dari bentuk geometri lainnya.
3. Keliling lingkaran dinyatakan sebagai 2πr, di mana π adalah pi (sekitar 3.14159). Keliling adalah panjang dari garis tepi lingkaran.
4. Luas lingkaran dinyatakan sebagai π, di mana π adalah pi dan r adalah jari-jari lingkaran. Ini adalah cara mengukur luas daerah yang dibatasi oleh tepi lingkaran.

baca juga : tutor private

Persamaan dalam Bentuk Lain: Selain bentuk umum, persamaan dapat dinyatakan dalam bentuk lain, seperti bentuk titik pusat-jari-jari atau bentuk standar (x – + (y – = . Kedua bentuk ini juga digunakan secara luas tergantung pada situasi matematika yang diberikan.

Interaksi Lingkaran dengan Garis: Persamaan lingkaran juga berperan penting dalam memecahkan masalah geometri yang melibatkan interaksi dengan garis. Misalnya, titik-titik potong antara garis dan lingkaran dapat dihitung dengan menggunakan persamaan lingkaran dan persamaan garis yang relevan.

Persamaan Lingkaran

A. Persamaan Jarak pada Lingkaran

1. Jarak titik (x₁,y₁) ke titik (x₂,y₂)

2. Jarak titik (x₁,y₁) ke garis Ax + By + C = 0

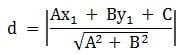
B. Persamaan Garis Singgung

Garis singgung ialah garis yang memotong lingkaran di satu titik. Ada tiga hal yang menentukan persamaan garis singgung, yaitu :

1. Apabila diketahui titik pada lingkaran

Ada titik (x₁,y₁) pada lingkaran, maka persamaannya harus diubah menjadi seperti berikut ini:

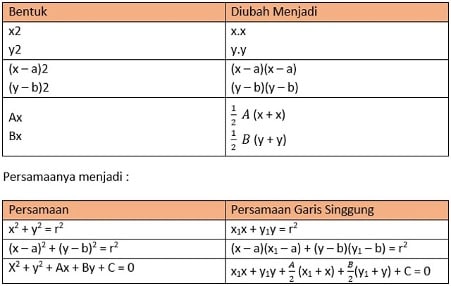
2. Apabila diketahui titik diluar lingkaran

• Tentukan persamaan garis kutub (poral) dari titik A(x₁,y₁) terhadap lingkaran.
• Melalui titik potong antara garis kutub lingkaran.
• Tentukan persamaan garis singgung melalui titik potong garis kutub.

3. Apabila diketahui gradien

Apabila telah diketahui titik (x₁,y₁) dengan gradien m pada lingkaran. Maka :

C. Kedudukan Dua Lingkaran

Jika jarang antara titik pusat lingkaran dituliskan d, serta r₂ dan r₂ adalah jari-jari pada masing-masing kedua lingkaran, maka kedua lingkaran tersebut akan saling :

• Saling lepas, sehingga d > r₁+ r₂
• Saling bersinggungan di dalam lingkaran, sehingga d = |r₁– r₂|
• Saling bersinggungan di luar lingkaran, sehingga d = r₁+ r₂
• Saling berpotongan, sehingga |r₁– r₂| < d < r₁ + r₂
• Lingkaran di dalam lingkaran, sehingga d = < r₁– r₂

baca juga : biaya les privat

Soal Pilihan Ganda

1.Sebuah lingkaran dengan pusat (1,2) memiliki jari-jari 5. Tentukan persamaan lingkaran tersebut!
Jawab :
p = (1,2) → pusat lingkaran (a,b)
r = 5

Karena pusat lingkaran (a,b), maka rumus persamaan yang digunakan adalah (x – a)²+ (y – b)² = r².
⇒ (x – a)² + (y – b)² = r²
⇒ (x – 1)² + (y – 2)² = 25

Berikutnya, konversikan bentuk standar ke dalam bentuk umumnya :
⇒ x² – 2x + 1 + y² – 4y + 4 = 25
⇒ x² + y² – 2x – 4y – 20 = 0

Jadi, bentuk umum persamaan lingkaran pusat (2,3) dan jari-jari 5 adalah x² + y² – 2x – 4y – 20 = 0

2. Persamaan lingkaran yang melalui titik (3,-2) dan memiliki titik pusat (3,4) adalah ….
Jawab :
Diketahui titik (3,-2) dan pusat (3,4)
Cari nilai r terlebih dahulu melalui rumus di bawah ini:
(x – a)² + (y – b)² = r²
(3 – 3)² + (-2 – 4)² = r²
0 + 36 = r²
r = √36
r = 6

Jadi persamaan lingkaran tersebut adalah :
(x – a)² + (y – b)² = r²
(x – 3)² + (y – 4)² = 6²
x² – 6x + 9 + y² – 8y + 16 = 36
x² + y² – 6x – 8y + 25 = 36
x² + y² – 6x – 8y – 11 = 0

baca juga : les privat jakarta

3. Tentukan persamaan lingkaran dengan pusat (1,2) dan memiliki jari-jari 5. Tentukan persamaan lingkarannya!

Jawab:

P = (1,2) → pusat lingkaran (a,b)

R  = 5

Karena pusat lingkarannya (a,b), maka kita gunakan aturan (x-a)²+(y-b)²=r².

(x-a)²+(y-b)²=r²

(x-1)²+(y-2)²=25

Selanjutnya, konversi bentuk standar ini ke dalam bentuk umumnya:

X²-2x+1+y²-4y+4=25

X²+y²-2x-4y-20=0

Sehingga, bentuk umum persamaan lingkaran dengan pusat (2,3) dan jari-jari 5 adalah x²+y²-2x-4y-20=0.

Jadi, apa lagi yang ditunggu? Hubungi kami segera di line telepon (021) 77844897 atau kamu juga bisa menghubungi kami via 0896-2852-2526. Atau klik www.simakui.id untuk mendapatkan informasi lebih lanjut.

Sampai ketemu di SIMAK UI

Referensi :

1. Latisprivat.com

2. Katadata.co.id