Halo sahabat Simak UI!
Transformasi geometri adalah konsep penting dalam matematika dan ilmu komputer yang memungkinkan kita untuk memahami perubahan bentuk dan ukuran objek dalam ruang. Transformasi ini digunakan dalam berbagai bidang, termasuk grafika komputer, ilmu fisika, teknik, dan banyak lagi. Dalam artikel ini, kita akan menjelajahi sifat-sifat transformasi geometri yang memungkinkan kita untuk memahami bagaimana objek dapat berubah dalam ruang.
baca juga : les privat
Apa itu Transformasi Geometri?

Sumber: Freepik
Transformasi geometri adalah konsep fundamental dalam matematika yang digunakan untuk mengubah bentuk, ukuran, dan posisi objek geometri dalam ruang. Ini adalah alat penting dalam matematika, fisika, komputer grafis, dan berbagai disiplin ilmu lainnya. Transformasi geometri memungkinkan kita untuk memahami perubahan dalam dunia nyata dan menyederhanakan analisis objek geometri.
Jenis-jenis Transformasi Geometri

Sumber: Freepik
Transformasi geometri dapat dibagi menjadi beberapa jenis utama, yaitu:
1. Translasi atau Pergeseran
Translasi adalah jenis transformasi yang mengubah posisi suatu objek geometri tanpa mengubah bentuk, ukuran, atau orientasinya. Dalam translasi, seluruh objek digeser oleh vektor tertentu, yang dapat dinyatakan sebagai perubahan dalam koordinat x, y, dan z. Translasi sering digunakan dalam pemodelan objek bergerak dalam matematika dan ilmu komputer.
Misalkan sobat punya sebuah titik T (x,y) yang ditranslasikan menurut (a,b) maka hasil setelah transfromasi adalah:
(x’,y’) = (x+a, y+b)
2. Refleksi atau Pencerminan
Refleksi adalah transformasi yang mencerminkan objek geometri terhadap sumbu tertentu. Sumbu refleksi adalah garis atau bidang yang digunakan sebagai cermin. Hasilnya adalah objek yang terlihat seperti pantulan simetris dari objek asli. Refleksi digunakan dalam simetri geometri dan dalam membuat objek bersifat simetris.
baca juga : les privat jakarta
Berikut tabel transformasi pencerminan:
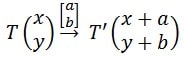
| Percerminan Terhadap |
Pemetaan | Matriks Transformasi |
| Sumbu x | (x,y) → (x,-y) | |
| Sumbu y | (x,y) → (-x,y) | |
| Garis x = y | (x,y) → (y,x) | |
| Garis x = -y | (x,y) → (-y,-x) | |
| Titik (0,0) | (x,y) → (-x,-y) | |
| Garis x = k | (x,y) → (2k-x,y) | |
| Garis y = k | (x,y) → (x,2k-y) | |
| Garis y = mx tan α |
X’ = x cos 2α + y sin 2α y’ = x sin 2α – y cos 2α |
3. Rotasi atau Perputaran
Rotasi adalah transformasi yang mengubah orientasi objek geometri dengan cara memutar objek tersebut sekitar titik tertentu yang disebut sebagai pusat rotasi. Sudut rotasi dan arah rotasi (searah jarum jam atau berlawanan) dapat diatur sesuai kebutuhan. Rotasi adalah komponen penting dalam pengolahan gambar, animasi, dan mekanika.
Ada dua macam rotasi, rotasi dengan titik pusat (0,0) dan rotasi dengan titik tertentu P (a,b).
a) Rotasi dengan Titik Pusat (0,0) dengan Sudut Putar α
![]()
Dimana
X’ = x cos α – y sin
y’ = x sin α + y cos α
Atau jika dibuat matriks transformasinya menjadi
![]()
Keterangan
Α bernilai + jika arah putaran berlawanan dengan arah jarum jam
α bernilai – jika araha putaran searah dengan arah jarum jam
b) Rotasi dengan Titik Pusat (a,b) dengan Sudut Putar α
Jika sobat punya sebuah titik (x,y) yang diputar sebesar α derajat dengant titik pusat P (a,b) maka:
![]()
Dimana
X’ – a = (x-a) cos α – (y-b) sin α
y’ – b = (x-a) sin α + (y-b) cos α
4. Dilatasi atau Perkalian
Dilatasi adalah transformasi yang mengubah ukuran objek geometri dengan cara memperbesar atau memperkecil objek tersebut relatif terhadap titik tertentu yang disebut sebagai pusat dilatasi. Faktor skala yang digunakan untuk dilatasi dapat lebih dari 1 (untuk memperbesar) atau antara 0 dan 1 (untuk memperkecil). Dilatasi digunakan dalam perubahan skala gambar dan pemodelan pertumbuhan atau penyusutan.
Faktor dilatasi dilambangkan dengan k dimana
- Jika k > 1 atau k <-1 maka diperbesar
- Jika -1 < k < 1 maka diperkecil
- Jika k = 1 atau k = -1 maka bangun tidak mengalami perubahan ukuran
baca juga : bimbel simak ui s2
- Dilatasi terhadap titik pusat O (0,0)Dilatasi dengan pusat O (0,0) dan faktor dilatasi K maka
- Dilatasi terhadap titik pusat P (a,b)Jika sebuah titik didilatasi dengan faktor dilatasi k dan titik pust P (a,b) ma

![]()
dimana
x’-a = k (x-a)
y’-b = k (y-b)
![]()
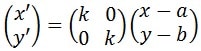
Penerapan Transformasi Geometri
Transformasi geometri memiliki banyak penerapan dalam dunia nyata, termasuk:
1. Grafika Komputer: Transformasi geometri digunakan untuk membuat animasi, rendering grafis, dan permainan komputer. Mereka memungkinkan perubahan posisi, rotasi, dan skala objek di layar.
2. Robotika: Dalam robotika, transformasi geometri digunakan untuk mengontrol pergerakan robot dan manipulatornya, sehingga mereka dapat berinteraksi dengan objek dalam lingkungan mereka.
3. Pemrosesan Citra: Dalam pemrosesan citra, transformasi digunakan untuk memperbaiki gambar, mengoreksi distorsi, dan mengubah ukuran gambar.
4. Rekayasa Struktural: Dalam rekayasa struktural, transformasi digunakan untuk menganalisis bagaimana struktur akan berperilaku di bawah beban atau tekanan tertentu.
5. Desain Arsitektur: Arsitek menggunakan transformasi geometri untuk merancang dan mengatur tata letak bangunan dan struktur.
Sifat-sifat Transformasi Geometri

Sumber: Freepik
-
Kesetaraan Jarak:
Dalam translasi, semua titik dalam objek bergerak dengan jarak dan arah yang sama. Ini berarti bahwa jarak antara semua pasangan titik dalam objek tetap sama setelah translasi.
-
Invariansi Sudut:
Dalam rotasi, sudut antara dua garis atau sudut antara dua vektor dalam objek tetap sama setelah transformasi. Ini berarti bahwa rotasi tidak mengubah sudut-sudut dalam objek.
-
Simetri:
Refleksi adalah transformasi trigonometri yang mempertahankan jarak dan sudut, tetapi mengubah arah objek. Objek yang simetris terhadap suatu sumbu akan tetap simetris setelah refleksi terhadap sumbu tersebut.
-
Perubahan Skala:
Dilatasi adalah transformasi trigonometri yang mengubah ukuran objek dengan faktor tertentu. Ini memengaruhi semua jarak dalam objek, sehingga memperbesar atau memperkecil objek dengan faktor tertentu.
-
Transformasi Proyeksi:
Proyeksi adalah transformasi trigonometri yang mengubah posisi objek ke dalam bidang tertentu atau mereduksi dimensinya. Ini sering digunakan dalam ilmu fisika dan grafika komputer untuk menciptakan efek perspektif.
Soal Pilihan Ganda

Sumber: Freepik
- Transformasi geometri yang mengubah bentuk suatu objek tanpa mengubah ukurannya disebut sebagai…
A) Translasi
B) Rotasi
C) Dilatasi
D) Refleksi
Jawaban yang benar adalah d) Refleksi.
Refleksi adalah transformasi geometri yang memantulkan objek melintasi suatu garis, tetapi tidak mengubah ukurannya.
- Jika suatu objek digeser sejajar sumbu x positif sebesar 5 unit dan sumbu y positif sebesar 3 unit, transformasi tersebut disebut sebagai….
A) Translasi
B) Rotasi
C) Dilatasi
D) Refleksi
Jawaban yang benar adalah a) Translasi.
Translasi adalah transformasi yang menggeser objek dalam ruang tanpa mengubah bentuk atau orientasi objek tersebut.
baca juga : tutor private
- Jika sebuah segitiga diputar sekitar titik tertentu, transformasi tersebut disebut sebagai….
A) Translasi
B) Rotasi
C) Dilatasi
D) Refleksi
Jawaban yang benar adalah b) Rotasi.
Rotasi adalah transformasi geometri yang mengubah orientasi objek dengan memutarnya sekitar titik tertentu.
- Jika sebuah objek diperbesar dengan faktor tertentu tanpa mengubah posisi pusatnya, transformasi tersebut disebut sebagai…
A) Translasi
B) Rotasi
C) Dilatasi
D) Refleksi
Jawaban yang benar adalah c) Dilatasi.
Dilatasi adalah transformasi yang mengubah ukuran objek dengan faktor tertentu tanpa mengubah posisi pusat objek.
- Transformasi yang memutar objek sekitar sumbu tertentu, misalnya sekitar sumbu x, sumbu y, atau sumbu z, disebut sebagai…
A) Translasi
B) Rotasi
C) Dilatasi
D) Refleksi
Jawaban yang benar adalah b) Rotasi.
Rotasi adalah transformasi yang memutar objek sekitar sumbu tertentu.
Jadi, apa lagi yang ditunggu? Hubungi kami segera di line telepon (021) 77844897 atau kamu juga bisa menghubungi kami via 0896-2852-2526. Atau klik www.simakui.id untuk mendapatkan informasi lebih lanjut.
Sampai ketemu di SIMAK UI
Referensi :
- kumparan.com
- supercampalumniui.com







